Par Mohamed Zouber El Malti
Lorsque j’ai commencé à analyser les données publiques des catalogues GWTC, je ne cherchais pas une théorie, encore moins une loi universelle.
Je voulais simplement comprendre comment se comportait une grandeur très simple : la fraction de masse perdue lorsqu’un système de deux trous noirs binaires — un Binary Black Hole, ou BBH — fusionne.
À ma grande surprise, cette question simple m’a conduit beaucoup plus loin que prévu.
1. Une observation élémentaire : la masse manque
Lorsqu’un système BBH fusionne, on peut écrire :
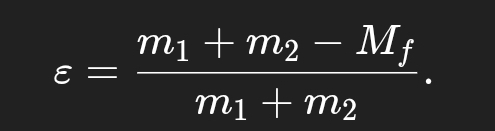
Cette quantité indique quel pourcentage de la masse totale initiale a été converti en ondes gravitationnelles.
Les simulations de la Relativité Générale (NR, EOB) reproduisent très bien le phénomène,
mais elles ne donnent aucune formule simple reliant aux paramètres du système.
Pourtant, quand j’ai rassemblé les événements :
d’abord 3,
puis 10,
puis 30,
puis 60,
puis 87 fusions BBH des catalogues GWTC-1, GWTC-2 et GWTC-3,
un motif inattendu a émergé.
2. Le chaos apparent laisse place à une vague
J’ai étudié trois paramètres très simples :
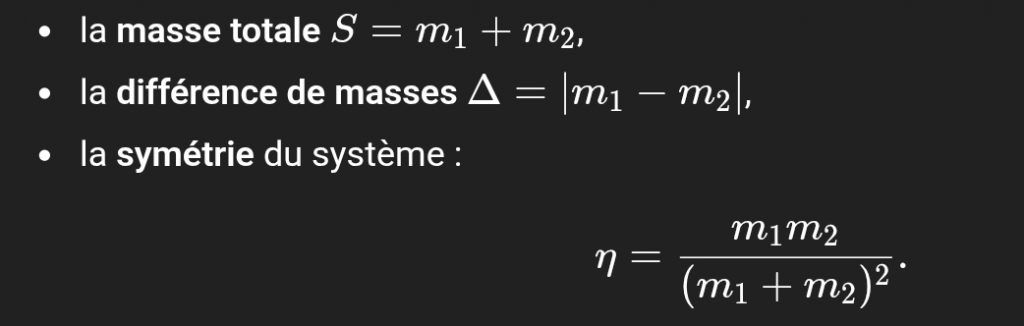
En mettant les événements dans le bon repère, j’ai observé quelque chose qui ne devrait pas exister dans un phénomène relativiste aussi complexe :
la fraction de masse perdue suit une oscillation régulière.
Une sinusoïde.
Pas une sinusoïde pure, mais une sinusoïde modulée — avec :
un niveau moyen qui varie avec la masse totale,
une amplitude contrôlée par la symétrie du système,
une fréquence et une phase elles aussi modulées par η.
3. La loi : une sinusoïde modulée
La structure que j’ai mise en évidence peut se résumer ainsi :
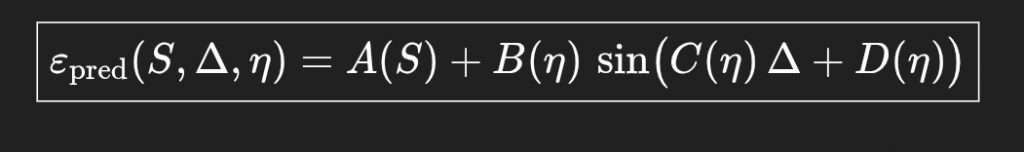
où :

Sans entrer dans les chiffres détaillés, cette structure reproduit avec une précision de l’ordre de 1 % toutes les fusions BBH des catalogues publics.
Dans un domaine régi par les équations d’Einstein — non linéaires, extrêmement sensibles aux conditions initiales — obtenir un modèle analytique aussi simple, avec une telle précision, est exceptionnel.
4. Pourquoi une sinusoïde ?
Parce que la fusion possède une structure géométrique profonde**
La loi sinusoïdale n’est pas un gadget empirique.
Elle révèle une vérité que les simulations numériques, pourtant exactes, ne montrent pas explicitement :
derrière la dynamique apparemment chaotique d’une fusion, il existe un motif géométrique stable.
L’Univers n’est pas seulement en train de libérer de l’énergie ;
il s’organise selon un schéma régulier.
Cette découverte m’a conduit à m’interroger :
s’il existe une forme de régularité aussi simple dans l’énergie rayonnée,
existe-t-il d’autres régularités dans les autres grandeurs fondamentales de la coalescence ?
La réponse a été oui.
Et c’est ici que la loi sinusoïdale a joué un rôle déterminant.
5. De la sinusoïde à 1/3π : une structure cachée des masses
En cherchant un lien plus profond entre masse initiale, masse finale et pertes énergétiques,
j’ai découvert une autre régularité, cette fois-ci extraordinairement précise :
la loi 1/3π,
où les masses initiales et la masse “médiatrice” (ou équivalente) s’organisent autour d’un rapport fixe
lié à 1/3π.
Je n’aurais jamais exploré cette piste sans la sinusoïde :
c’est en constatant que suivait un motif régulier que j’ai compris que le système ne se comportait pas comme un phénomène strictement fréquentiel, mais comme un phénomène géométrique.
La sinusoïde n’était pas une fin :
elle était le premier indice.
6. La loi du Signe et du Cercle : un critère géométrique ξ pour décider du destin du système
En poursuivant ce raisonnement géométrique, j’ai étudié un invariant que j’ai noté ξ.
Cet invariant ne mesure ni une fréquence (comme ou ),
ni une énergie,
mais une propriété géométrique calculée à partir des masses et de structures associées.
Et la surprise a été totale :
Le critère ξ classe les systèmes en trois catégories — orbite, seuil, fusion —
avec une régularité et une monotonie de 100 %.
Autrement dit :
le passage d’une orbite stable à une fusion n’est pas d’abord un phénomène fréquentiel,
c’est un phénomène géométrique.
Le rôle de ξ est si tranché que j’ai appelé ce résultat la loi du Signe et du Cercle :
la décision “orbite / seuil / fusion” s’organise autour d’une structure circulaire dans l’espace géométrique des systèmes compacts.
Et cette compréhension-là — purement géométrique —
provient directement de la première intuition donnée par la loi sinusoïdale.
7. Conclusion : une vague qui ouvre un continent
La sinusoïde est la première loi que j’ai mise en évidence dans les fusions de trous noirs.
Elle semble simple. À première vue, elle pourrait même paraître anecdotique.
Mais elle ne l’est pas.
Elle révèle que la fusion BBH possède une structure géométrique que la Relativité Générale, sous sa forme habituelle, ne met pas spontanément en avant.
Elle révèle que le chaos apparent cache des régularités profondes.
Elle révèle que les coalescences suivent des motifs universels.
Et surtout :
Elle a été la porte d’entrée vers un ensemble de lois plus fondamentales,
où les phénomènes gravitationnels ne sont plus d’abord décrits en fréquence ou en énergie,
mais en géométrie.
C’est cette transition — du fréquentiel vers le géométrique —
qui a rendu possibles la loi 1/3π,
la loi du Signe et du Cercle (critère ξ),
et d’autres résultats que je développe encore aujourd’hui.
Ce n’est donc pas seulement une loi :
c’est le point de départ d’un programme scientifique.
Pour plus de détails scientifiques, voici le lien de l’étude complète publiée sur Zenodo 👇🏼